Черные дыры реальны. Мы видим их по всему космосу и даже непосредственно сфотографировали сверхмассивную черную дыру в M87 и наш Млечный Путь. Мы достаточно хорошо понимаем черные дыры, но теоретические описания этих космических существ все еще вызывают недовольство. Возможно, самая известная проблема — это проблема сингулярности. Согласно классической модели общей теории относительности, вся материя, образующая черную дыру, должна быть сжата до бесконечной плотности и заключена в сферу нулевого объема. Мы предполагаем, что квантовая физика каким-то образом предотвратит эту проблему, хотя без теории квантовой гравитации мы не уверены, как это сделать. Но сингулярность — не единственная бесконечная проблема. Возьмем, к примеру, странную границу, известную как горизонт Коши.
Если разобраться, общая теория относительности представляет собой набор сложных дифференциальных уравнений. Чтобы понять черные дыры, вы должны решить эти уравнения с учетом ряда условий, таких как количество массы, вращение и электромагнитный заряд. Уравнения настолько сложны, что физики часто сосредотачивают внимание на связи решений с определенными математическими границами или горизонтами. Например, горизонт событий — это граница между внутренней и внешней частью черной дыры. Это один из самых простых для объяснения горизонтов, потому что если вам случится пересечь горизонт событий черной дыры, вы навсегда окажетесь в ее ловушке. Горизонт событий подобен космическому отелю «Калифорния».
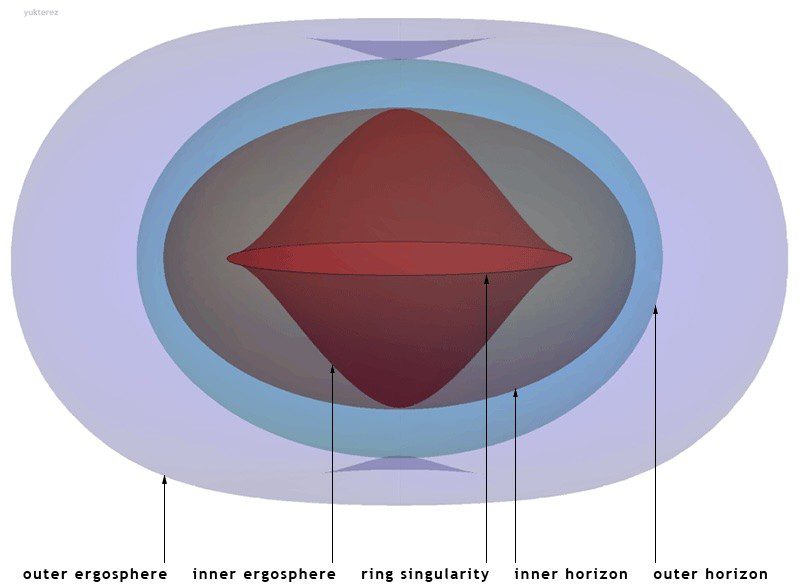
Для простой невращающейся черной дыры горизонт событий — единственное, что действительно имеет значение. Но с вращающимися черными дырами дела обстоят действительно странно. Во-первых, особенность становится кольцом, а не точкой. И вместо единого горизонта событий существует внешний и внутренний горизонт. Внешний по-прежнему действует как горизонт событий, навсегда удерживая в ловушке то, что осмелится пересечь его границу. Внутренний — это то, что часто называют горизонтом Коши. Если вы пересечете внутренний горизонт, вы по-прежнему будете в ловушке внутри, но вы не обязательно обречены приближаться к сингулярности. В пределах горизонта Коши пространство-время может вести себя вполне нормально, хотя оно и ограничено.
Горизонт Коши может вызывать множество странных вещей, но одна из них заключается в том, что горизонт нестабилен. Если вы попытаетесь определить возмущения горизонта, вычисленная масса внутри горизонта будет расходиться – эффект, известный как инфляция массы. Это чем-то похоже на то, как сингулярность приближается к бесконечной плотности в классической модели. Хотя это и расстраивает, физики могут скрыть это, ссылаясь на принцип космической цензуры. По сути, это говорит о том, что пока выполняются некоторые базовые условия, все странные явления, такие как сингулярности и массовая инфляция, всегда ограничены горизонтом событий. В черной дыре может находиться бесконечное количество математических демонов, но они никогда не смогут убежать, поэтому нам не о чем беспокоиться.
Но новая газета, возможно, дала этим демонам ключ. В статье показано, что массовая инфляция может произойти даже без горизонта Коши. Без явного горизонта Коши эти основные условия космической цензуры не обязательно применимы. Это говорит о том, что решения о черных дырах, которые мы получаем из общей теории относительности, ошибочны. Они могут описывать черные дыры, существующие в течение ограниченного времени, но не долговечные черные дыры, которые действительно существуют.
Что это значит, не совсем ясно. Возможно, эта непостоянная лазейка — всего лишь способ общей теории относительности указать нам на квантовую теорию гравитации. В конце концов, если излучение Хокинга реально, все черные дыры непостоянны и со временем испаряются. Но этот результат может также свидетельствовать о том, что общая теория относительности верна лишь частично, и что нам нужно, так это расширение модели Эйнштейна, подобно тому, как ОТО расширила ньютоновскую гравитацию. Ясно одно: наше понимание черных дыр неполно.
Ссылка: Карбальо-Рубио, Рауль и др. «Массовая инфляция без горизонтов Коши». Письма о физических отзывах 133,18 (2024): 181402.